Количество ситуаций в методе Джессики Фридрих на кубике Рубика 3х3 и шанс скипа

 Решил написать эту статью ради интереса. Получилась длинная, но надеюсь что она будет Вам интересна.

Все результаты в статье получены этим вечером.

Приступим!

---

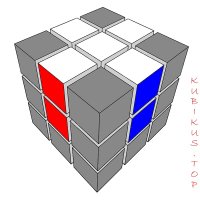
Количество возможных видов крестов на кубике Рубика 3х3
Для начала, количество перестановок 4-х рёбер:
12*11*10*9

И каждое ребро может быть перевернуто в 2-х позициях:
2^4

Теперь нужно разделить на 24, чтобы зафиксировать куб (тогда мы получаем только количество видов крестов относительно любого цвета).
КРЕСТ: 12*11*10*9*2^4/24 = 7,920 ситуаций.

---

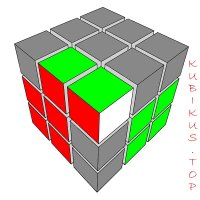
Количество Ф2Л позиций и видов Ф2Л пар

Вам тоже было интересно, сколько нужно знать алгоритмов сборки, чтобы решать Ф2Л за один алгоритм?

Поехали. Будем считать по каждой паре отдельно:

1 пара:
Ребро может находится в 8 позициях и может быть перевернуто двумя способами: 8*2

Угол тоже в 8, но 3-мя способами: 8*3

8*2*8*3 = 384 видов Ф2Л пар существует.


Но решить мы можем каждую в 4 разных слота:

• 1-я пара: 384*4 = 1,536 ситуаций;
• 2-я пара: 7*2*7*3*3 = 882 ситуаций;
• 3-я пара: 6*2*6*3*2 = 432 ситуаций;
• 4-я пара: 5*2*5*3 = 150 ситуаций.

Тогда получается:

Общее количество ситуаций в Ф2Л:
1,536*882*432*150 = 87,787,929,600 ситуаций.


87 миллиардов! 

Так что алгоритмами не обойдёшься, придётся опять улучшать лукехед.

---

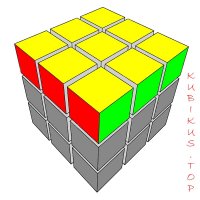
Количество ситуаций на ОЛЛ, ПЛЛ, ЛЛ

ОЛЛ (OLL): 
Ориентация углов 3*3*3 = 27

Четвёртый угол зависит от трех:
Ориентация ребер 2*2*2 = 8

Четвёртое ребро зависит от трех:
ОЛЛ (OLL): 8 * 27 = 3^3 * 2^3 = 216 ситуаций.

ПЛЛ (PLL):
Перестановки ребер 3*2 = 6
(на 4 не умножаем, потому что нужно "закрепить" верхнюю грань, убрать доворот)

Перестановки углов 4*3 = 12

Поскольку в кубике Рубика 3х3 не может быть нечётное количество перестановок, то на 2 умножить нельзя.
ПЛЛ: 3*2*4*3 = 4!*3 = 72 ситуаций.

ЛЛ (LL): 216*72 = 15,552 ситуаций.

---

Количество доворотов при сборке кубика Рубика 3х3

Ну, тут все очевидно: 4 ситуации.

ИТОГ:
В этом списке указано количество разнообразных ситуаций для каждого этапа сборки кубика Рубика 3 на 2 (например, доворот + плл - тоже отдельная ситуация).
По этому же списку можно судить о шансе скипа каждого этапа, просто поделите единицу на нужное число.


ЭТАП: КОЛИЧЕСТВО СИТУАЦИЙ.

• КРЕСТ: 7,920;
• 1-я ПАРА: 1,536;
• 2-я ПАРА: 882;
• 3-я ПАРА: 432;
• 4-я ПАРА: 150;
• ОЛЛ: 216;
• ПЛЛ: 72;
• ДОВОРОТ: 4.

Проверим:
7,920*1,536*882*432*150*216*72*4 = 43,252,003,274,489,856,000 ситуаций на кубике Рубика 3х3.

Мы вышли на это число, все сошлось. 

Спасибо за то, что уделили время на прочтение.

---

Автор идеи и статьи @AndrejK1